Hendrik Fischer
Publications

Publications

Hendrik Fischer, Julian Roth, Ludovic Chamoin, Amelie Fau, Mary F. Wheeler, and T. Wick
In this work, the space-time MORe DWR (Model Order Reduction with Dual-Weighted Residual error estimates) framework is extended and further developed for single-phase flow problems in porous media. Specifically, our problem statement is the Biot system which consists of vector-valued displacements (geomechanics) coupled to a Darcy flow pressure equation. The MORe DWR method introduces a goal-oriented adaptive incremental proper orthogonal decomposition (POD) based-reduced-order model (ROM). The error in the reduced goal functional is estimated during the simulation, and the POD basis is enriched on-the-fly if the estimate exceeds a given threshold. This results in a reduction of the total number of full-order-model solves for the simulation of the porous medium, a robust estimation of the quantity of interest and well-suited reduced bases for the problem at hand. We apply a space-time Galerkin discretization with Taylor-Hood elements in space and a discontinuous Galerkin method with piecewise constant functions in time. The latter is well-known to be similar to the backward Euler scheme. We demonstrate the efficiency of our method on the well-known two-dimensional Mandel benchmark and a three-dimensional footing problem.

Hendrik Fischer, Julian Roth, Thomas Wick, Ludovic Chamoin, and Amelie Fau
In this work, the dual-weighted residual (DWR) method is applied to obtain a certified incremental proper orthogonal decomposition (POD) based reduced order model. A novel approach called MORe DWR (Model Order Rduction with Dual-Weighted Residual error estimates) is being introduced. It marries tensor-product space-time reduced-order modeling with time slabbing and an incremental POD basis generation with goal-oriented error control based on dual-weighted residual estimates. The error in the goal functional is being estimated during the simulation and the POD basis is being updated if the estimate exceeds a given threshold. This allows an adaptive enrichment of the POD basis in case of unforeseen changes in the solution behavior which is of high interest in many real-world applications. Consequently, the offline phase can be skipped, the reduced-order model is being solved directly with the POD basis extracted from the solution on the first time slab and — if necessary — the POD basis is being enriched on-the-fly during the simulation with high-fidelity finite element solutions. Therefore, the full-order model solves can be reduced to a minimum, which is demonstrated on numerical tests for the heat equation and elastodynamics.

Niklas Kühl, Hendrik Fischer, Micheal Hinze, and Thomas Rung
The paper presents a strategy to construct an incremental Singular Value Decomposition (SVD) for time-evolving, spatially 3D discrete data sets. A low memory access procedure for reducing and deploying the snapshot data is presented. Considered examples refer to Computational Fluid Dynamic (CFD) results extracted from unsteady flow simulations, which are computed spatially parallel using domain decomposition strategies. The framework addresses state of the art PDE-solvers dedicated to practical applications. Although the approach is applied to technical flows, it is applicable in similar applications under the umbrella of Computational Science and Engineering (CSE). To this end, we introduce a bunch matrix that allows the aggregation of multiple time steps and SVD updates, and significantly increases the computational efficiency. The incremental SVD strategy is initially verified and validated by simulating the 2D laminar single-phase flow around a circular cylinder. Subsequent studies analyze the proposed strategy for a 2D submerged hydrofoil located in turbulent two-phase flows. Attention is directed to the accuracy of the SVD-based reconstruction based on local and global flow quantities, their physical realizability, the independence of the domain partitioning, and related implementation aspects. Moreover, the influence of lower and (adaptive) upper construction rank thresholds on both the effort and the accuracy are assessed. The incremental SVD process is applied to analyze and compress the predicted flow field around a Kriso container ship in harmonic head waves at Fn = 0.26 and ReL = 1.4E+07. With a numerical overhead of O(10%), the snapshot matrix of size O(R10E+08 x 10E+04) computed on approximately 3000 processors can be incrementally compressed by O(95%). The storage reduction is accompanied by errors in integral force and local wave elevation quantities of O(1E-02%).

Hendrik Fischer, Amelie Fau, and Thomas Wick
In this work, we apply reduced-order modeling to the parametrized, time-dependent, incompressible, laminar Navier-Stokes equations. The major goal is to reduce the computational costs by replacing the high-fidelity system by a low-rank approximation, which preserves the solution behavior. We utilize projection-based reduced basis methods and carry out the basis generation by POD-greedy sampling. Both a velocity-only and a velocity-pressure reduced-order model are considered, with the latter stabilized by means of supremizer enrichment. Here, we investigate further reduction possibilities. We present numerical results of the method applied to the benchmark problem of a two-dimensional flow around a cylinder with physical parametrization.

Hendrik Fischer (Master Thesis)
The classical POD algorithm requires the complete flow field to be available beforehand. This requirement makes the method inappropriate for the unsteady adjoint-based optimization, as it also results in a memory exhaustion. Therefore, the objective of this thesis is to develop an incremental variant of the POD such that the reduced primal field can be computed in a computational efficient way on the fly during the primal computation.
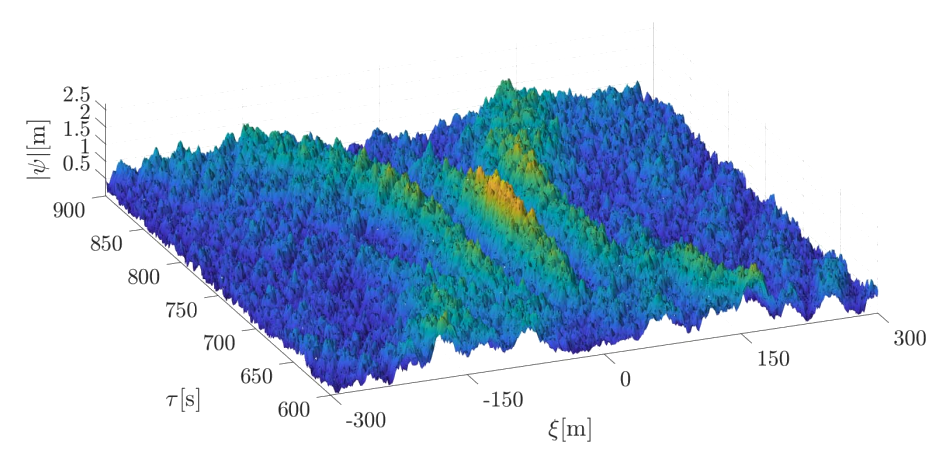
Hendrik Fischer, Marten Hollm, and Leo Dostal
Although extreme or freak waves are repeatedly measured in the oceans, their origin is largely unknown. The interaction of different water waves is seen as one reason for their emergence. One way to consider nonlinear waves in deep water is to look at solutions of the nonlinear Schrödinger equation, which plays an important role in the determination of extreme waves. One specific solution is the soliton solution. Therefore the question arises, how nonlinear waves behave as they interact or collide. Using a relaxation pseudo spectral scheme for the computation of solutions of the nonlinear Schrödinger equation, the behavior of colliding solitons is studied. Thereby, different wave amplitudes and angles of collision are considered. In addition to this, the influence of an initial perturbation by random waves is studied, which is generated using a Pierson-Moskowitz spectrum.

Marten Hollm, Leo Dostal, Hendrik Fischer, and Robert Seifried
The nonlinear Schrödinger equation plays an important role in wave theory, nonlinear optics and Bose-Einstein condensation.Depending on the background, different analytical solutions have been obtained. One of these solutions is the soliton solution.In the real ocean sea, interactions of different water waves can be observed at the surface. Therefore the question arises, howsuch nonlinear waves interact. Of particular interest is the interaction, also called collision, of solitons and solitary waves. Using a spectral scheme for the numerical computation of solutions of the nonlinear Schrödinger equation, the nonlinearwave interaction for the case of soliton collision is studied. Thereby, the influence of an initial random wave is studied, whichis generated using a Pierson-Moskowitz spectrum.